在此感谢本文主要笔者 25 级 xiaozhangup

图解二维差分和前缀和

前情提要

本文档中所有表格的左上角格子定义为 (0, 0)，暂且把它称为 原格；表格的最左上角的点，我们把它称为 原点。向右和向下为正方向。
本文旨在通过几何图像直观介绍二维前缀和和差分的概念，仅关注 “它是什么” 和 “它表示什么” ，不涉及具体代码实现细节。
你必须先理解一维前缀和和一维差分才可以顺畅阅读本教程。

对于二维前缀和

我们如图定义一个 5*5 的二维数值矩阵，这也将是我们存储前缀和的矩阵。

那么，前缀和是什么？
简单概括一下：

1
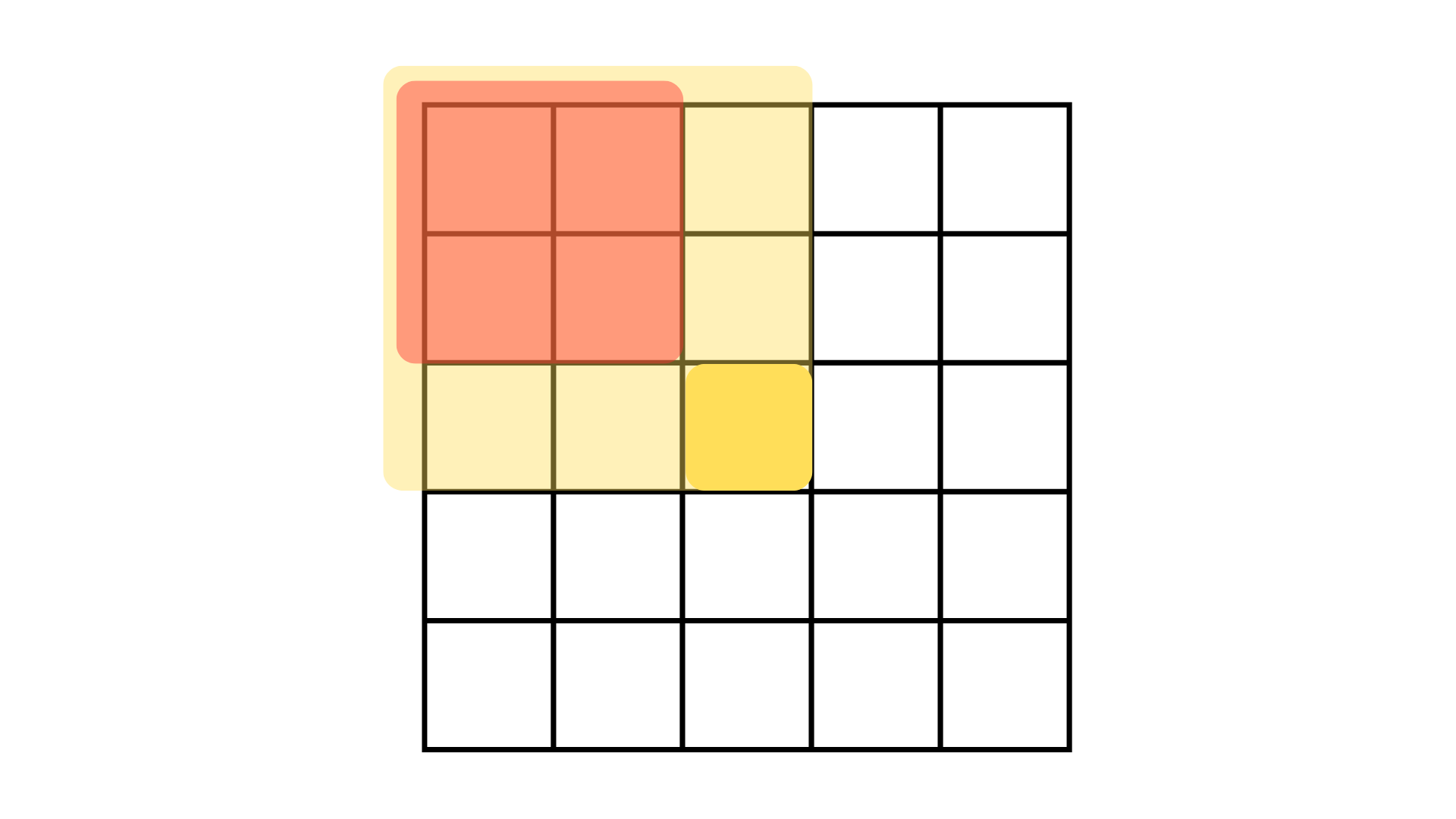
2

我们定义黄色色块所在的格子是 (x,y)，那么:
黄色格子(x,y) 内的数值就是从 ```原数组``` 的原格到黄色格子(x,y) ，所覆盖的格子(红色+黄色) 内的所有数字的和。

来用一个更好懂的图片来描述：
从黄色格子(x, y) 作为原格右下角点出发，向其左和上方做射线，所形成的区域包含的所有格子内 原数组数值 的和就是这个黄色格子内的数值，我们给出两个例图：

这就是前缀和二维数组中每个格子的含义。
那么，快速求和是什么逻辑？
我们可以把它简单理解为图形的割补。
现在，抛开之前的所有定义，我们仅仅从几何的角度来进行分析：

1 2	我每次只能切或者补一个一定包含原点为其其中一个顶点的矩形，我们需要几步把图中的这个灰色矩形切出来？

很简单，按照如图的 3 步即可达到我们的目的！
第一步：
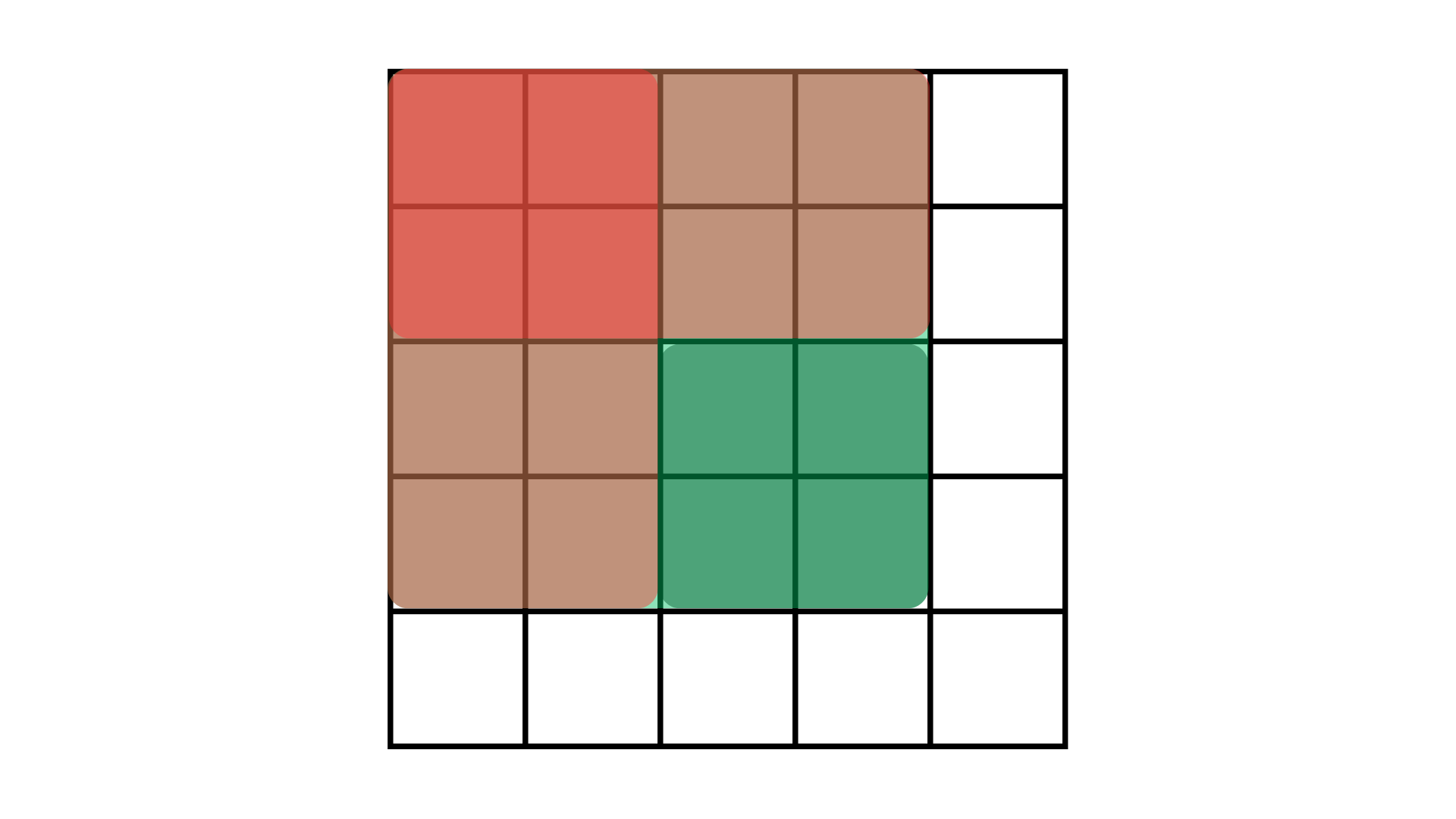
取全部的绿色部分

第二步：
割掉红色的那两个部分
初见端倪，为什么左上角颜色更深？
因为左上角那一块我们切割了两次！

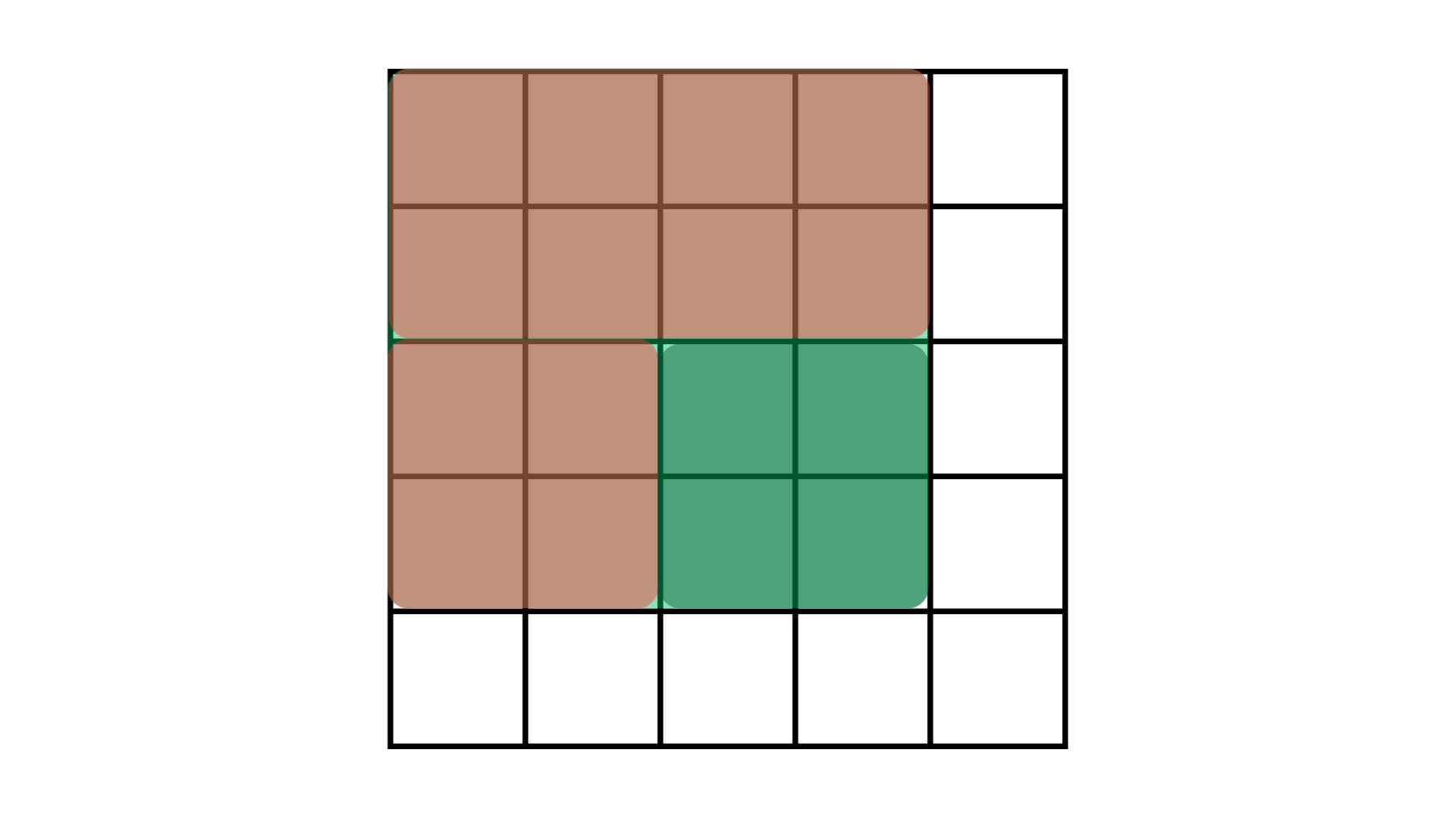
第三步：
把切割了两次的红色区域补上一块 (红色变浅了)。
如此一来，剩下的绿色不就是我们想要的区域了吗？

那么，根据我们切割的步骤，把他用数学逻辑表示出来：

S(绿色的面积) = S(绿色右下角点到原点构成的矩形) - S(绿色左下角点到原点构成的矩形) - S(绿色右上角点到原点构成的矩形) + S(绿色左上角点到原点构成的矩形)

我们这里所谓的 “面积”，不正是前缀和矩阵中格子的数值吗？
用程序代码表示一下，那就是：

int prefix[5][5];

// x1, y1, x2, y2 分别是矩形左上角和右下角坐标
// 这里的算式和上面的文字顺序是一一对应的
int sum(int x1, int y1, int x2, int y2) {
    return prefix[x2][y2] - prefix[x1 - 1][y2] - prefix[x2][y1 - 1] + prefix[x1 - 1][y1 - 1];
}

如此一来，我们就完成了区域的和计算。

对于二维差分

我们如图定义一个 5*5 的二维数值矩阵，这也将是我们存储二维差分的矩阵。

那么，差分是什么？
简单概括一下：

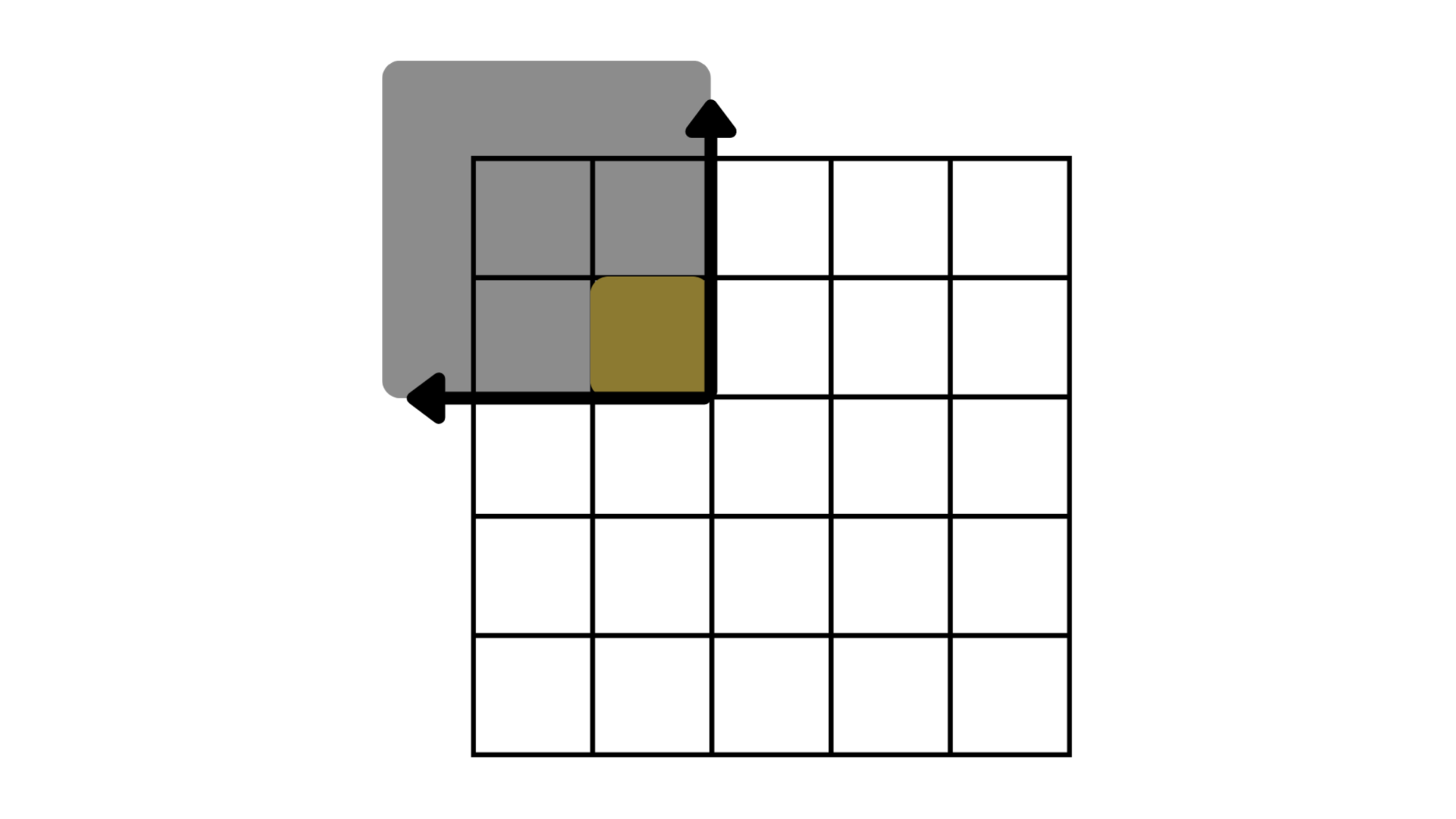
我们定义黄色色块所在的格子是 (x,y)，那么:
黄色格子(x,y) 内的数值就是被黄色覆盖的 ```原数组``` 内的所有数字和相较于被红色覆盖的 ```原数组``` 内的所有数字和的变化量。
例如红色部分的和是 18，黄色部分的和是 20，多了 2，那么 ```差分数组``` 中黄色格子内的值就是 +2；
如果红色部分的和是 18，黄色部分的和是 16，少了 2，那么 ```差分数组``` 中黄色格子内的值就是 -2；

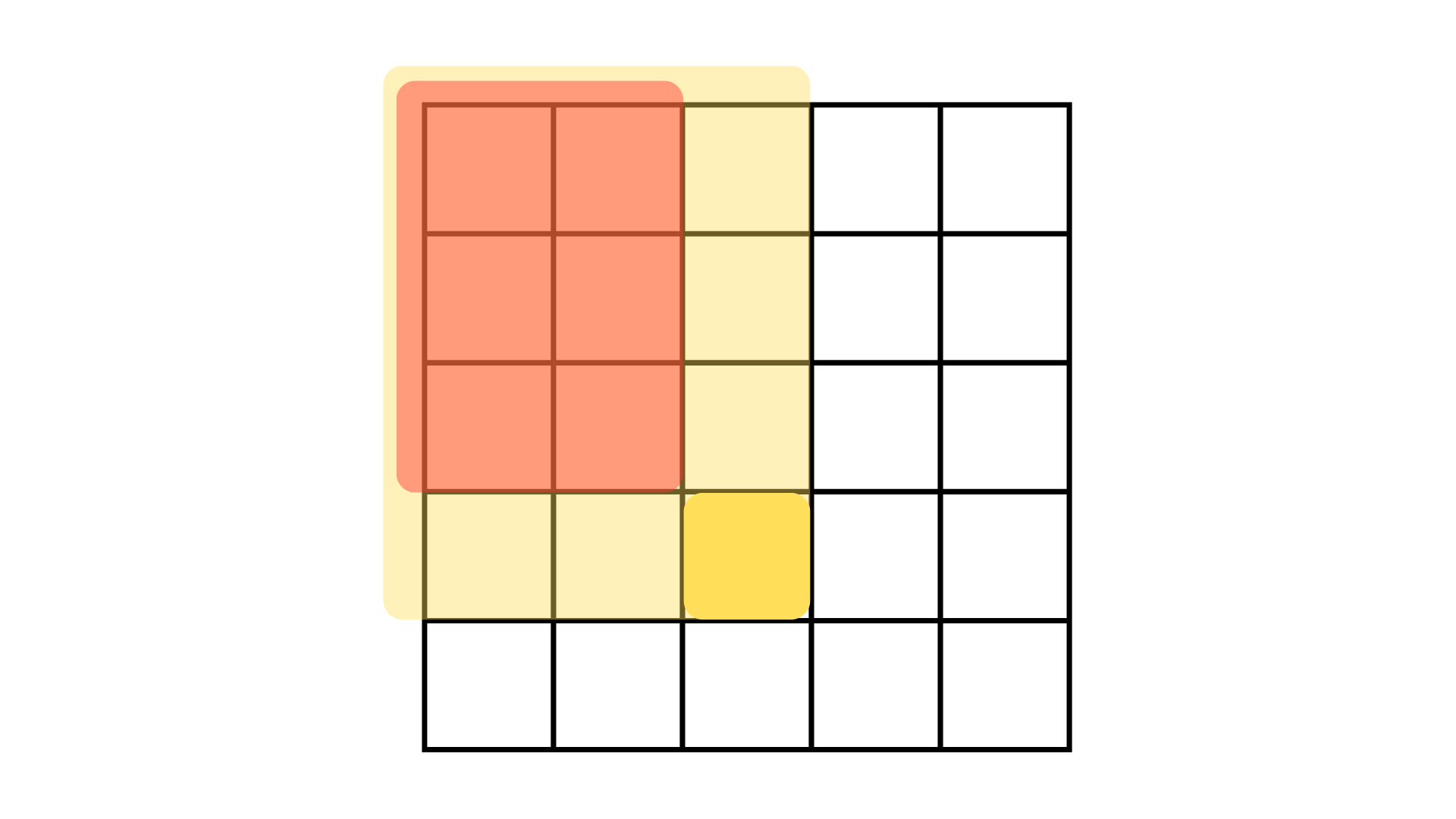
这就是差分二维数组中每个格子的含义。

那么，快速批量修改数组中间的某一块的数值是什么逻辑？
我们只需要记住这一点就可以快速理解二位差分的原理了：
对每一个格子操作所带来的影响都是面性的，影响其右下角范围内的所有格子

看图更易于理解：
这里我们假设我们修改了黄色格子内的差分数值，那么被该修改影响的矩形范围如下(类似前缀和，这里也是射线！)

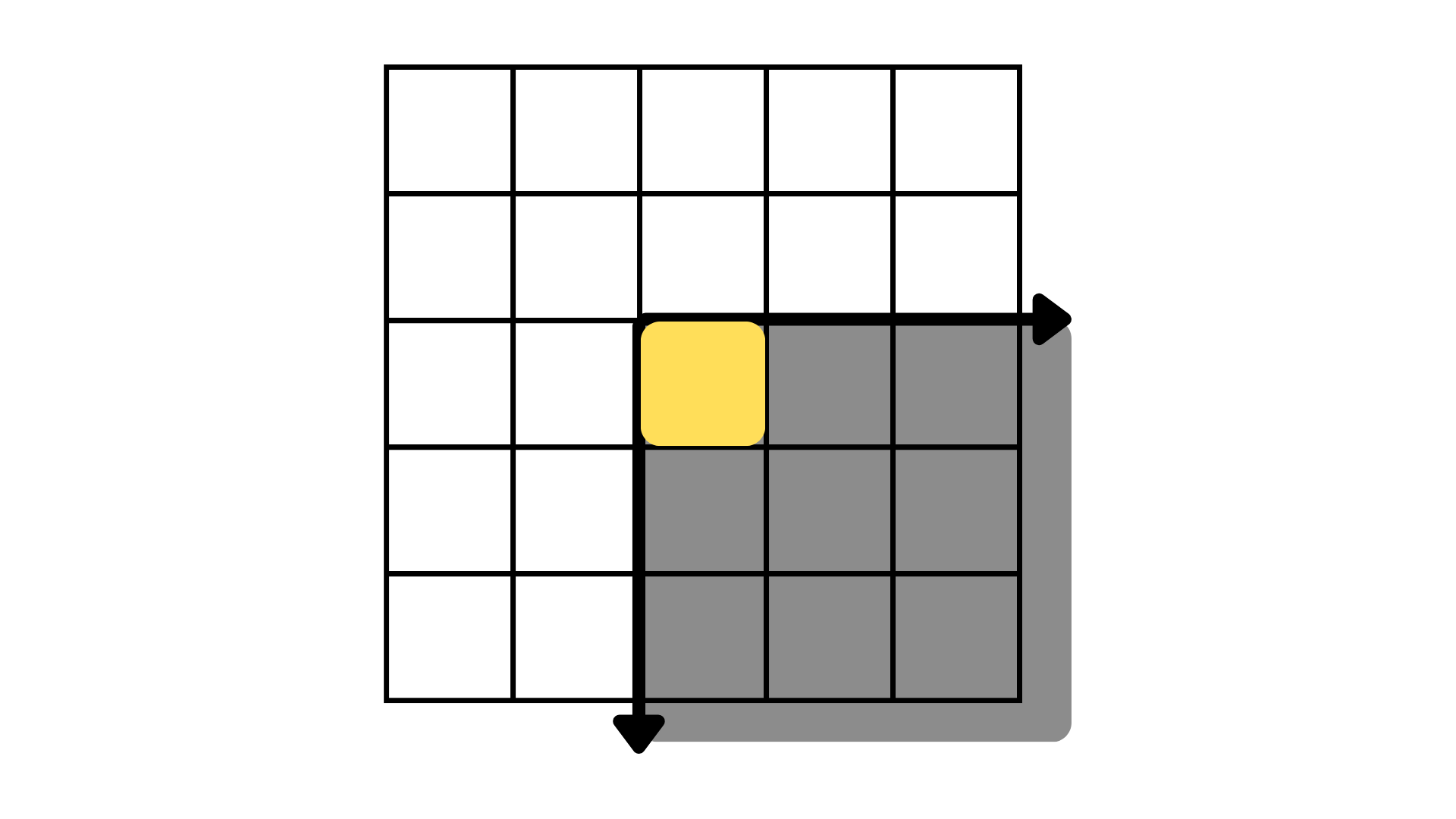
如果我们对黄色 +8，那么灰色区域全部都会被 +8。这一整个面内的格子都被抬升了 8。
相反的，如果我们对黄色 -8，那么灰色区域全部都会被 -8。这一整个面内的格子都被下降了 8。

那么，范围性修改又是怎么做到的呢？
现在再次忘掉前缀和，只关注最简单的平面几何：

1 2	我每次只能切或者补一个无限向右下角延申的矩形，需要几步把图中的这个灰色矩形切出来？

和我们前面对前缀和的几何化理解逻辑一样，但这次我们更自由了，不需要盯着原点不放了。

依然只需要三步，和之前大同小异！
第一步：
从灰色矩形的左上角点取全部的矩形

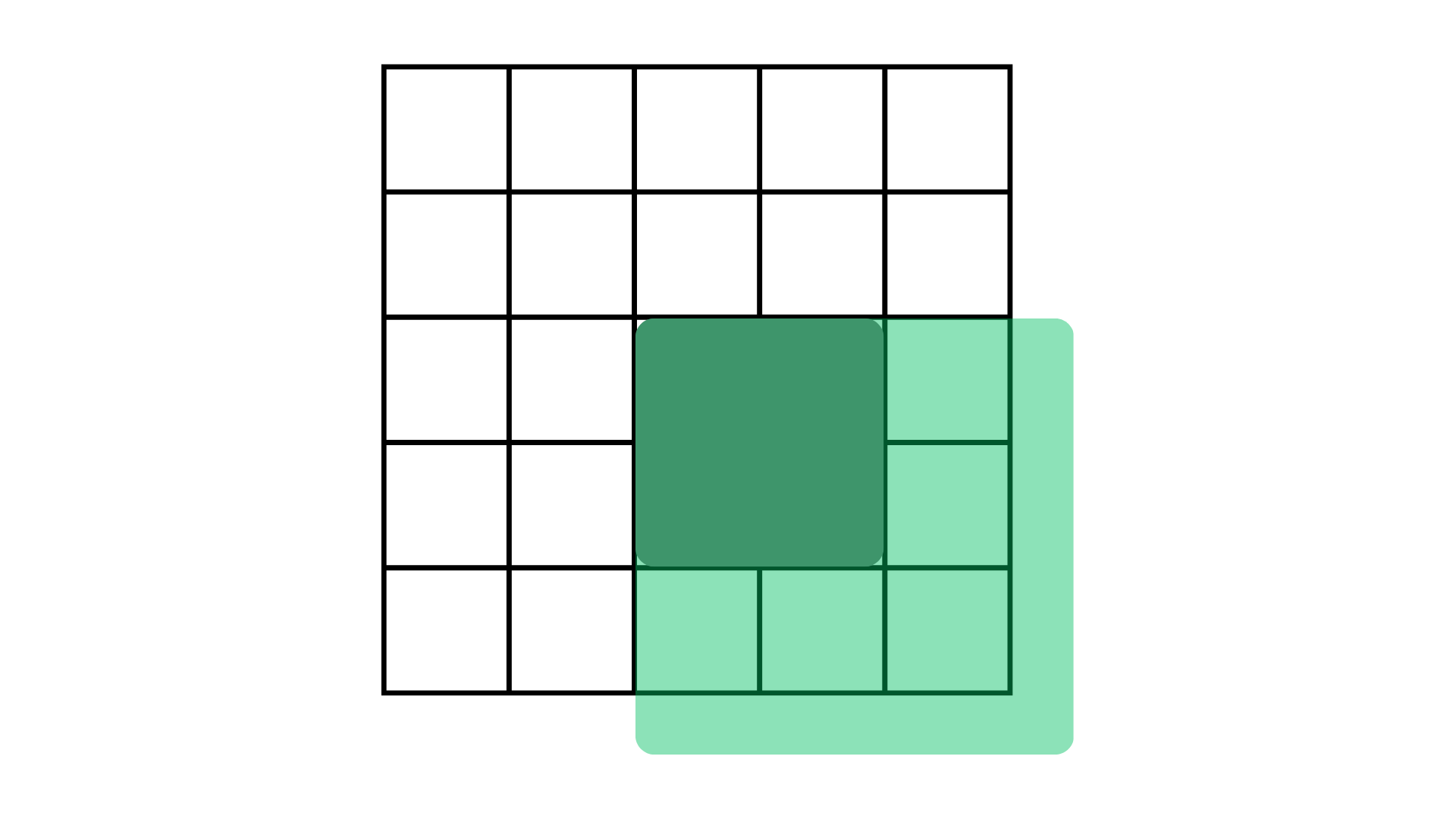
第二步：
从灰色的右上角点和左下角点取两个矩形割掉
再见端倪，为什么右下角颜色更深？
因为右下角那一块我们切割了两次！

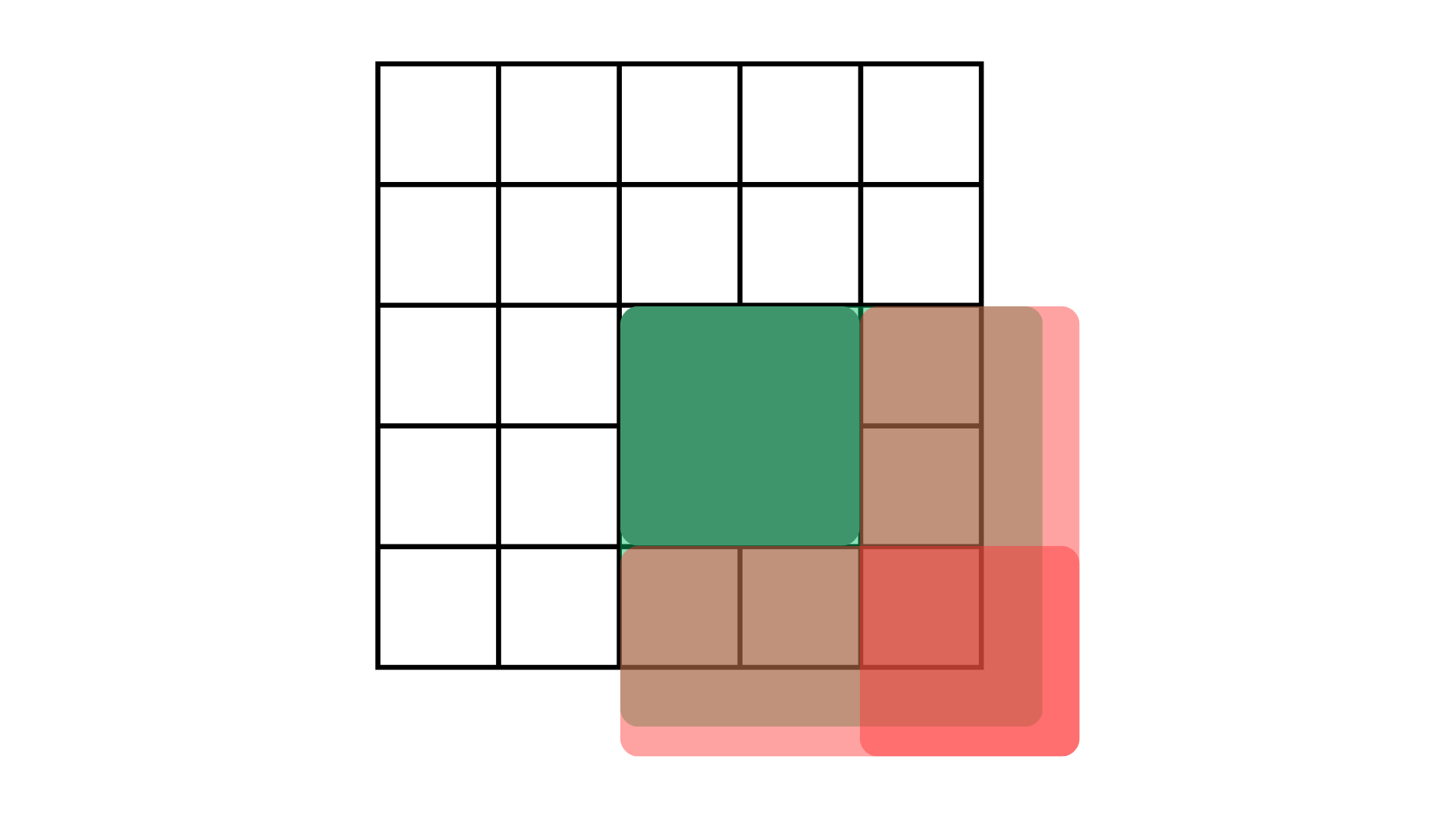
第三步：
把切割了两次的右下角区域补上一块 (右下角变浅了)。
类似我们取绿色块的操作，给变浅的那一块加上这个数即可影响到右下角的所有被切割了两次的块。

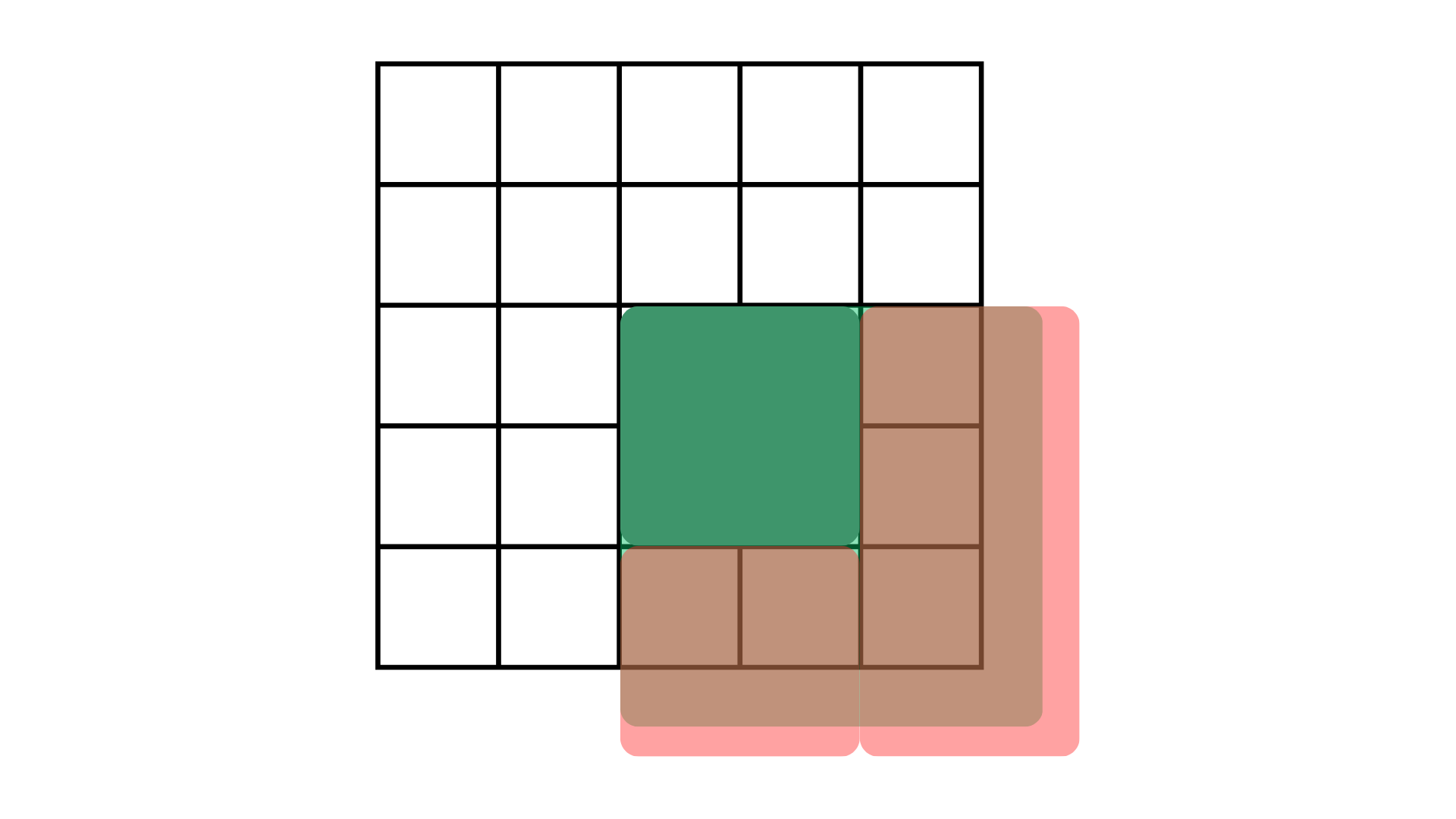
红绿重叠的部分相互抵消 (因为我们加减了相同的数值)，现在只剩下原先的灰色块了。
至此，区域修改完成！只有我们想要的格子们被改变，其他格子没有被改变。

如图中那样，我们其实只改变了四个格子的数值：

灰色块中的左上块
灰色块中右上块的右边一块
灰色块中左下块的下边一块
灰色块中右下块的右下块
用程序代码来表示一下：

int diff[5][5];

// x1, y1, x2, y2 分别是灰色块左上角和右下角坐标
// val 是你修改的数值
// 这里的修改顺序和上面的文字顺序是一一对应的
void add(int x1, int y1, int x2, int y2, int val) {
    diff[x1][y1] += val;
    diff[x2 + 1][y1] -= val;
    diff[x1][y2 + 1] -= val;
    diff[x2 + 1][y2 + 1] += val;
}

如此一来，我们就完成了差分的区域修改。

图解二维差分和前缀和

图解二维差分和前缀和

前情提要

对于二维前缀和

对于二维差分

教程完，感谢阅读！